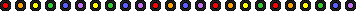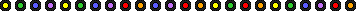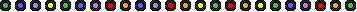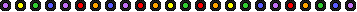La Regola dell'11 risale al 1889 e si deve allo scozzese Robert Foster e all'inglese E. M. F. Benecke che la scoprirono quasi in contemporanea applicandola al Whist, perché a quel tempo il Bridge stava ancora muovendo i suoi primi passi.

La Regola trova applicazione esclusivamente se si adotta la convenzione di attaccare dalla quarta carta di un seme almeno quarto e, generalmente, viene usata quando gli avversari sono impegnati in un contratto a SA anche se se ne può trarne indubbia utilità anche nel gioco a colore.

Oggi giorno l'attacco di 4ª carta non è più molto diffuso perché, a ragione, si ritiene che le informazioni che fornisce possono essere  utili più spesso al dichiarante che ai difensori.

Questo non toglie che la regola scoperta dai due britannici ha l'indubbio pregio di essere il primo esempio di approccio scientifico applicato al gioco della carta.

La Regola recita che: 

 La Regola dell'11 in difesa

Entriamo subito in argomento con un esempio:

Ovest attacca dalla quarta carta del suo colore più lungo con il 5 e il morto risponde passando il 7.

Est sottrae il valore della carta d'attacco (5) al numero "fisso 11" e trova 6, questo è il numero delle carte più alte di quella di attacco possedute dagli altri tre giocatori (escluso l'attaccante); dato che il 7 e l'8 sono visibili al morto e che la Dama ed il 9 sono nella sua mano, con una semplice sottrazione (6 - 4 = 2) Est può dedurre che Sud possiede due sole carte superiori a quella d'attacco.

Considerato che quattro delle sei carte superiori a quella d'attacco sono note (D, 9, 8, 7), Est può, inoltre, facilmente dedurre che il giocante è in possesso di due tra le seguenti carte: A, K,J, T, 6. 

Est può trarre un vantaggio decisivo da una informazione così limitata?

Analizziamo i 10 casi che si possono configurare mettendo in evidenza quelli nei quali Ovest avrebbe probabilmente scelto un attacco diverso:

Nel primo caso, Ovest avrebbe forse attaccato di Asso o di Re.

Comunque, in questi primi tre casi, se Est passa la Dama e ritorna nel colore realizza tutte le prese; se Est avesse, invece, passato il 9, EO avrebbero realizzato una presa in meno.

Il primo caso di questa nuova terna prevede un attacco di Fante o di Dieci (a seconda delle convenzioni adottate).

Negli altri due, se Est passa la Dama Sud la prende con il Re e, successivamente quando uno qualsiasi degli opponenti rientrerà in presa, EO incasseranno le rimanenti quattro prese (da notare che se Sud liscia la Dama, blocca le comunicazioni interne dei difensori).

Se Est avesse passato il 9 sull'attacco, Sud lo avrebbe preso con l’onore minore e così facendo avrebbe sguarnito solo a metà la sua tenuta, perché, tutte le volte che entra in presa Ovest, non può tornare nel colore senza regalare il Re.

Il primo caso di questa ultima quaterna prevede un attacco di Fante o di Dieci (a seconda delle convenzioni adottate).

Nei due casi centrali, se Est passa la Dama e Sud non prende, Est insiste nel colore e Sud perde le prime due prese prima di realizzare quella di Asso ma, almeno, riesce a sezionare il colore interrompendo le comunicazioni avversarie nel seme. Questa modo di manovrare permetterà a Sud di non perdere altre prese in questo colore se, in seguito, Ovest non dovesse riuscire a tornare in presa. Se Est avesse passato il 9 sull'attacco, Sud avrebbe realizzato nel colore di attacco una presa che non era di sua spettanza ed avrebbe mantenuto il controllo del colore

Nell’ultimo caso la carta passata da Est è ininfluente sul risultato finale (due prese per il giocante), salvo la considerazione che, se Sud vuole interrompere le comunicazioni tra i difensori, deve stare basso un giro anche in questa occasione.

Ricapitolando, se Est utilizza con raziocinio le informazioni che gli fornisce la Regola dell'11, passa la Dama anziché il 9 e, così facendo, agisce per il suo meglio.

Se ripetete per conto vostro l'intero ragionamento e ricostruite tutti gli schemi, supponendo che Ovest abbia attaccato dalla quarta carta di un suo colore quarto, vi renderete conto meglio del vantaggio che può derivare dall'applicazione della regola.

In questa combinazione, Ovest attacca con il 6 (che è la quarta carta) e Nord passa l'8, cosa deve fare Est per il suo meglio?

Applicare la Regola dell'11 naturalmente. Uhm, vediamo:

11 - 6 = 5

sono le carte superiori a quella d'attacco tra NS ed Est; due di queste sono in bella vista al morto (Q e 8) e tre sono nella mano di Est, ergo, a Sud non resta nessuna carta superiore al 6! ed Est può tranquillamente impegnare il 9 e proseguire prima con il Re e, poi, con il Dieci.

Al povero Sud non resterà che assistere sconsolato agli opponenti che incassano subito le cinque prese di loro spettanza.

Ecco come avrebbero potuto stare le cose:

e se Est avesse passato il Re per poi tornare nel colore, Sud avrebbe realizzato una presa che non gli spettava.

 La Regola dell'11 in attacco

Dato che ogni medaglia ha il suo rovescio, il giocante può trarre utili informazioni dall’attacco operato secondo la Regola dell’11:

Ovest attacca di 7 dalla quarta migliore del suo seme più lungo, quale carta deve chiamare Sud dal morto?

Applicando la Regola dell'11 la risposta è facile ed univoca:

11 - 7 = 4

sono le carte superiori a quella di attacco nelle mani di Nord, Sud ed Est; due di queste sono ben in vista al morto e altre due sono nella mano del giocante, ergo, Est ha solo carte inferiori a quella di attacco e, pertanto, Sud può limitarsi a chiamare tranquillamente il 3 dal morto, per fare la presa con il 9 della mano e, poi, una volta riscosso l'Asso, muovere il 4 dalla mano verso il Fante del morto per incassare le restanti due prese.

Ecco come avrebbero potuto stare le cose: